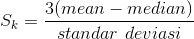BAB V

ARTIKEL STATISTIKA BAB V. Moment, Kemiringan dan Kurtosis

 ARTIKEL STATISTIKA

BAB V. MOMENT, KEMIRINGAN DAN KURTOSIS

Skewness and Kurtosis

Rata-rata dan ukuran penyebaran dapat menggambarkan distribusi data tetapi tidak cukup untuk menggambarkan sifat distribusi. Untuk dapat menggambarkan karakteristik dari suatu distribusi data, kita menggunakan konsep-konsep lain yang dikenal sebagai kemiringan (skewness) dan keruncingan (kurtosis).

Skewness

Kemiringan (skewness) berarti ketidaksimetrisan. Sebuah distribusi dikatakan simetris apabila nilai-nilainya tersebar merata disekitar nilai rata-ratanya. Sebagai contoh, distribusi data berikut simetris terhadap nilai rata-ratanya, 3.

x	1	2	3	4	5
frek (f)	5	9	12	9	5

Pada contoh gambar berikut, distribusi data tidak simetris. Gambar pertama miring (menjulur) ke arah kiri dan gambar ke-2 miring ke arah kanan.

Pada distribusi data yang simetris, mean, median dan modus bernilai sama.

Beberapa langkah-langkah perhitungan digunakan untuk menyatakan arah dan tingkat kemiringan dari sebaran data. Langkah-langkah tersebut diperkenalkan oleh Pearson.

Koefisien kemiringan(Coefficient of Skewness):

Interpretasi: Untuk distribusi data yang simetris, Sk = 0. Apabila distribusi data menjulur ke kiri (negatively skewed), Sk bernilai negatif, dan apabila menjulur ke kanan (positively skewed), SK bernilai positif. Kisaran untuk SK antara -3 dan 3.

Ukuran kemiringan yang lain adalah koefisien β₁ (baca 'beta-satu'):

dimana:

Interpretasi:

Distribusi dikatakan simetris apabila nilai b₁ = 0. Skewness positif atau negatif tergantung pada nilai b₁ apakah bernilai positif atau negatif.

Ukuran Skewness yang sering digunakan:

Skewness Populasi:

Skewness Sampel:

Source: D. N. Joanes and C. A. Gill. "Comparing Measures of Sample Skewness and Kurtosis". The Statistician 47(1):183–189.

atau formula berikut (MS Excel):

s = standar deviasi

NB: kedua formula di atas menghasilkan nilai skewness yang sama

Interpretasi:

Distribusi dikatakan simetris apabila nilai g₁ = 0. Skewness positif atau negatif tergantung pada nilai g₁ apakah bernilai positif atau negatif.

Menurut Bulmer, M. G., Principles of Statistics (Dover, 1979):

• highly skewed: jika skewness kurang dari −1 atau lebih dari +1
• moderately skewed: jika skewness antara −1 dan −½ atau antara +½ dan +1.
• approximately symmetric: jika skewness is berada di antara −½ dan +½.

Kurtosis

Kurtosis merupakan ukuran untuk mengukur keruncingan distribusi data.

Distribusi pada gambar di atas semuanya simetris terhadap nilai rata-ratanya. Namun bentuk ketiganya tidak sama. Kurva berwarna biru dikenal sebagai mesokurtik (kurva normal), kurva berwarna merah dikenal sebagai leptokurtik (kurva runcing) dan kurva berwarna hijau dikenal sebagai platikurtik (kurva datar).

Kurtosis dihitung dengan menggunakan koefisien Pearson, β₂ (baca 'beta - dua').

dimana:

Ukuran Kurtosis yang sering digunakan:

Kurtosis Populasi:

Kurtosis:

Excess Kurtosis: 

Kurtosis Sampel:

atau formula berikut (MS Excel):

s = standar deviasi

NB: Excel menggunakan nilai Excess Kurtosis. Hasil perhitungan dari kedua formula di atas, menghasilkan nilai yang sama

Interpretasi:

Distribusi dikatakan:

• Mesokurtik (Normal) jika b₂ = 3
• Leptokurtik jika b₂ > 3
• platikurtik jika b₂ < 3

Analisis Korelasi Product Moment dalam Statistika

Analisis korelasi merupakan salah satu teknik statistik yang digunakan untuk menganalisis hubungan antara dua variabel atau lebih yang bersifat kuantitatif. Salah satu dari analisis korelasi tersebut adalah analisis korelasi product moment (Pearson). Variabel yang digunakan disini terbagi dua yaitu variabel bebas (x) dengan variabel terikat (y), dengan ketentuan data memiliki syarat-syarat tertentu.

Korelasi Pearson Product Moment (r) dapat diformulasikan sbb:



dengan ketentuan −1 ≤ r ≤ r . Dan interpretasi koefisien korelasi nilai r ini dapat dirangkum dalam tabel berikut:



Langkah-langkah yang diperlukan untuk uji korelasi Pearson Product Moment adalah sebagai berikut :

1. Rumuskan hipotesis Ha dan Ho dalam bentuk kalimat.
2. Rumuskan hipotesis Ha dan Ho dalam bentuk statistik.
3. Buat tabel pembantu.
4. Tentukan r
5. Tentukan nilai KP
6. Lakukan uji signifikansi.
7. Tentukan α , dengan derajat bebas db = n − 2 .
8. Tentukan konklusi

BAB VI

ARTIKEL STATISTIKA BAB VI. Distribusi Normal, Distribusi T, dan Distribusi F

ARTIKEL STATISTIKA

BAB VI. DISTRIBUSI NORMAL, DISTRIBUSI T, dan DISTRIBUSI F

DISTRIBUSI NORMAL

Distribusi normal adalah distribusi dari variabel acak kontinu.  Kadang-kadang distribusi normal disebut juga dengan distribusi Gauss.  Distribusi ini merupakan distribusi yang paling penting dan paling banyak digunakan di  bidang statistika.

Fungsi densitas distribusi normal diperoleh dengan persamaan sebagai berikut:

dimana
π = 3,1416
e = 2,7183
µ = rata-rata
σ = simpangan baku
Persamaan di atas bila dihitung dan diplot pada grafik akan terlihat seperti pada Gambar 1 berikut:

  

Gambar 1. kurva distribusi normal umum

Sifat-sifat penting distribusi normal adalah sebagai berikut:

1. Grafiknya selalu berada di atas sumbu x

2. Bentuknya simetris pada x = µ

3. Mempunyai satu buah modus, yaitu pada x = µ

4. Luas grafiknya sama dengan satu unit persegi, dengan rincian

a. Kira-kira 68% luasnya berada di antara daerah µ – σ dan µ + σ

b. Kira-kira 95% luasnya berada di antara daerah µ – 2σ dan µ + 2σ

c. Kira-kira 99% luasnya berada di antara daerah µ – 3σ dan µ + 3σ

Membuat kurva normal umum bukanlah suatu pekerjaan yang mudah.  Lihat saja rumus untuk mencari fungsi densitasnya (nilai pada sumbu Y) begitu rumit.  Oleh karena itu, orang tidak banyak menggunakannya.

Orang lebih banyak menggunakan DISTIBUSI NORMAL BAKU.  Kurva distribusi normal baku diperoleh dari distribusi normal umum dengan cara transformasi nilai x menjadi nilai z, dengan formula sbb:

Kurva distribusi normal baku disajikan pada Gambar 2 berikut ini.

Gambar 2.  Kurva distribusi normal baku

Kurva distribusi normal baku lebih sederhana dibanding kurva normal umum.  Pada kurva distribusi normal baku, nilai µ = 0 dan nilai σ=1, sehingga terlihat lebih menyenangkan.  Namun, sifat-sifatnya persis sama dengan sifat-sifat distribusi normal umum.

Untuk keperluan praktis, para ahli statistika telah menyusun Tabel distribusi normal baku dan tabel tersebut dapat ditemukan hampir di semua buku teks Statistika.  Tabel distribusi normal bakui disebut juga dengan Tabel Z dan dapat digunakan untuk mencari peluang di bawah kurva normal secara umum, asal saja nilai µ dan σ diketahui. Sebagai catatan nilai µ dan σ dapat diganti masing-masing dengan nilai dan S.

 Distribusi t

Distribusi t merupakan salah satu pengembangan dari Distribusi z. Secara prinsip penggunaan Distribusi t digunakan untuk membandingkan rata-rata dari dua sampel. Rata-rata dua sampel tersebut dibandingkan untuk mengetahui apakah dua data tersebut mempunyai beda. Distribusi biasanya digunakan untuk data yang banyak sampelnya kurang dari sama dengan 30.

t di definisikan sebagai berikut:

Dari definisi nilai t di atas, ada beberapa nilai yang perlu kita ketahui:

sehingga inputan data di atas sebaiknya anda tahu.

Contoh ada nilai siswa sebagai berikut:

Nilai
66
40
75
64
65
71
66
81
65
50

Apakah nilai data tersebut rata-ratanya sama dengan data yang lain yang rata-ratanya 60?
Dari data di atas diperoleh nilai sebagai berikut:

Misalkan taraf signifikansinya 0.05, nilai derajat kebebasan data tersebut dk = 10 - 1 = 9. Dari tabel distribusi t didapatkan :

Sedangkan nilai t hitung bisa diperoleh dari :

Dari nilai tersebut diperoleh

Kesimpulannya data diatas tidak berbeda signifikan dengan data yang rata-rata populasinya 60.

Distribusi F (ANOVA)

            ANOVA kepanjangan dari Analysis of Variance. Distribusi yang ditemukan oleh seorang ahli statistika bernama R.A Fisher pada tahun 1920. Distribusi F (ANOVA) adalah prosedur statistika untuk menghitung apakah rata-rata hitung drai 3 populasi atau lebih sama atau tidak. Distribusi ini digunakan untuk menguji rata-rata dari tiga atau lebih populasi sekaligus untuk menentukan apakah rata-rata itu sama atau tidak.
            Distribusi F (ANOVA) terbagi menjadi 2 klasifikasi:

1. Klasifikasi satu arah

Klasifikasi satu arah adalah sebuah klasifikasi pengmatan yang hanya didasarkan pada satu kriteria.

     2.  Klasifikasi dua arah 

Klasifikasi dua arah adalah suatu pengamatan yang didasarkan pada dua kriteria seperti varietas dan jenis pupuk.suatu pengamatan dapat diklasifikasikan menurut dua criteria dengan menyusun data tersebut menjadi baris dan kolom, kolom menyatakan kriterika klasifikasi yang satu sedangkan baris menyatakan criteria klasifikasi yang lainnya.

MOMEN, KEMENCENGAN DAN KURTOSIS

1.  PENDAHULUAN

Rata-rata dan varians sebenarnya merupakan hal istimewa dari kelompok ukuran

lain yang disebut momen. Dari momen ini pula beberapa ukuran lain dapat diturunkan.

Bentuk-bentuk sederhana  dari  momen  dan  ukuran-ukuran  yang didapat  daripadanya

akan diuraikan di dalam bab ini.

2.  MOMEN

Misalkan diberikan variable  x dengan harga-harga:  x₁,  x₂,  ….,  x_n.  Jika  A  =

sebuah  bilangan tetap dan r = 0, 1, 2, ……., n, maka  momen ke-r  sekitar  A, disingkat

mr, didefinisikan oleh hubungan:

(1) ……………………………

 = Σ(        )

Untuk A = 0 didapat momen ke-r sekitar nol atau disingkat momen ke-r:

(2) ……………………………

−     =

Dari  rumus  (2),  maka  untuk r  =  1  didapat  rata-rata  ̅ .  Jika  A  = ̅   kita  peroleh

momen ke-r sekitar rata-rata, biasa disingkat dengan m_r. Jadi didapat:

(3) …………………………...

=⁽̅ )

Untuk r = 2, rumus (3) memberikan varians s².

Untuk membedakan apakah momen itu untuk sampel atau untuk populasi, maka

dipakai simbul:

m_r dan m_r untuk momen sampel dan _r dan _r untuk momen populasi.

Jadi, m_r dan m_r adalah statistik sedangkan _r dan _r merupakanparameter.

Jika data telah disusun dalam daftar distribusi  frekuensi,  maka rumus-rumus di

atas berturut-turut berbentuk:

(4) ………………………..  

(5) ………………………..               

(6) ………………………..  

= Σ    (         )

−     =

=⁽̅ )

dengan n = f_i, x_i = tanda kelas interval dan f_i = frekuensi yang sesuai dengan x_i.

Dengan menggunakan cara sandi, rumus 4 menjadi:

(7) ………………………

dengan, p = panjang kelas interval,  

=

c_i = variable sandi.

 Dari      ,  harga-harga  m_r  untuk beberapa  harga  r,  dapat ditentukan  berdasarkan

hubungan:

=         −   (     )

=         −  3

=         − 4

+ 2(      )

+ 6(       )

− 3(       )

Contoh: Untuk menghitung empat buah momen sekitar rata-rata untuk data dalam daftar

distribusi frekuensi, kita lakukan sebagai berikut.

DATA

60 – 62

63 – 65

66 – 68

69 – 71

72 - 74

Jumlah

f_i

5

18

42

27

8

100

c_i

-2

-1

0

1

2

-

f_ic_i

-10

-18

0

27

16

15

20

18

0

27

32

97

-40

-18

0

27

64

33

80

18

0

27

128

253

=

Dengan menggunakan rumus (7), maka:

= 3            = 0,45

=

= 3

= 8,73

=

= 3

= 8,91

=

= 3

= 204,93

Sehingga dengan menggunakan hubungan di atas:

=         −   (     ) = 8,73 −   (0,45) = 8,53.

=         −  3

+ 2(       ) = 8,91 − 3(0,45)(8,73) + 2(0,45) = −2,69

=         − 4

+ 6(       )

− 3(       )

= 204,93 − 4(0,45)(8,91) + 6(0,45) (8,73) − 3(0,45) = 199,38

Dari hasil ini, didapat varians s² = m₂ = 8,53.

3.  KEMENCENGAN

Kemencengan  atau kecondongan  (skewness)  adalah  tingkat ketidaksimetrisan

atau kejauhan simetri dari sebuah distribusi. Sebuah distribusi yang tidak simetris akan

memiliki  rata-rata,  median,  dan  modus  yang tidak sama  besarnya  (      ≠ Me  ≠  Mo),

sehingga distribusi akan terkonsentrasi pada salah satu sisi dan kurvanya akan menceng. 

Jika distribusi memiliki ekor yang lebih panjang ke kanan daripada yang ke kiri

maka  distribusi  disebut  menceng ke  kanan  atau memiliki  kemencengan positif.

Sebaliknya,  jika  distribusi  memiliki  ekor  yang lebih panjang ke  kiri daripada  yang ke

kanan maka distribusi disebut menceng ke kiri atau memiliki kemencengan negatif.

Berikut  ini  gambar  kurva  dari  distribusi  yang menceng  ke  kanan (menceng

positif) dan menceng ke kiri (menceng negatif).

Mo         

 Gambar a  

Gambar 1

                   Mo

          Gambar b

Kemencengan Distribusi (a) Menceng ke kanan (b) Menceng ke kiri

Untuk mengetahui  bahwa  konsentrasi  distribusi  menceng  ke  kanan atau

menceng ke kiri, dapat digunakan metode-metode berikut :

1.    Koefisien Kemencengan Pearson

Koefisien Kemencengan Pearson merupakan nilai selisih rata-rata dengan modus

dibagi simpangan baku. Koefisien Kemencengan Pearson dirumuskan sebagai berikut:

−

= 

Keterangan :

sk = koefisien kemencengan Pearson

Apabila secara empiris didapatkan hubungan antar nilai pusat sebagai :

−

= 3(     −       )

Maka rumus kemencengan di atas dapat diubah menjadi :

3(    −       )

= 

Jika nilai sk dihubungkan dengan keadaan kurva maka :

1) sk = 0

kurva memiliki bentuk simetris;

2) sk> 0

3)  sk< 0

Contoh soal :

nilai-nilai terkonsentrasi pada  sisi sebelah kanan  (  terletak di  sebelah

kanan  Mo), sehingga kurva memiliki ekor memanjang ke kanan, kurva

menceng ke kanan atau menceng positif;

nilai-nilai terkonsentrasi pada sisi sebelah kiri (  terletak di sebelah kiri

Mo), sehingga kurva memiliki ekor memanjang ke kiri, kurva menceng

ke kiri atau menceng negatif.

Berikut ini adalah data nilai ujian statistik dari 40 mahasiswa sebuah universitas.

Nilai Ujian Statistika pada Semester 2, 2010

Nilai Ujian

31 – 40

41 – 50

51 – 60

61 – 70

71 – 80

81 – 90

91 – 100

Jumlah

Frekuensi

4

3

5

8

11

7

2

40

a)  Tentukan nilai sk dan ujilah arah kemencengannya (gunakan kedua rumus tersebut) !

b) Gambarlah kurvanya !

Penyelesaian:

Nilai

31 – 40

41 – 50

51 – 60

61 – 70

71 – 80

81 – 90

91 – 100

Jumlah

X

35,5

45,5

55,5

65,5

75,5

85,5

95,5

f

4

3

5

8

11

7

2

40

u

-4

-3

-2

-1

0

1

2

u²

16

9

4

1

0

1

4

fu

-16

-9

-10

-8

0

7

4

-32

fu²

64

27

20

8

0

7

8

134

∑

  =      +       ∑     = 75,5 + 10

−32

40     = 75,5 − 8 = 67,5 

   =

∑

1

−

∑

= 10

134

40  −

1

−32

40       = 10 (1,62) = 16,2

  =      +

2    − (∑     )_.= 60,5 +  ²(40) − 12 . 10 = 60,5 + 10 = 70,5

8

4

  =     +₊.                  = 70,5 +  4 + 5  . 10 = 70,5 + 4,44 = 74,94

a.

= 

=  ^,

,

,

=   −0,46

 Oleh  karena  nilai  sk-nya  negatif  (-0,46)  maka  kurvanya  menceng ke  kiri  atau

menceng negatif.

b.  Gambar kurvanya :

Kurva nilai ujian statistik

12

10

8

6

4

2

0

35

45

56

66

Gambar 2

76

86

96

2.    Koefisien Kemencengan Bowley

Kurva menceng ke kiri

Koefisien kemencengan Bowley berdasarkan pada hubungan kuartil-kuartil (Q₁,

Q₂ dan Q₃) dari sebuah distribusi. Koefisien kemencengan Bowley dirumuskan :

(      −      ) − (       −      )

=

atau

(      −      ) + (       −      )

− 2      +

=

−

Keterangan : sk_B

=  koefisien kemencengan Bowley;

Q = kuartil

Koefisien  kemencengan  Bowley  sering juga  disebut  Kuartil Koefisien

Kemencengan.Apabila nilai sk_B dihubungkan dengan keadaan kurva, didapatkan :

1) Jika Q₃ – Q₂ > Q₂ – Q₁ maka distribusi akan menceng ke kanan atau menceng secara

positif.

2)  Jika Q₃ – Q₂ < Q₂ – Q₁  maka distribusi akan  menceng ke kiri atau menceng secara

negatif.

3) sk_B positif, berarti distribusi mencengke kanan.

4) sk_B negatif, nerarti distribusi menceng ke kiri.

5)  sk_B  =  ±  0,10 menggambarkan  distribusi  yang menceng  tidak berarti  dan sk_B>  0,30

menggambarkan kurva yang menceng berarti.

Contoh soal :

Tentukan kemencengan kurva dari distribusi frekuensi berikut :

Nilai Ujian Matematika Dasar I dari 111 mahasiswa, 1997

Penyelesaian :

Nilai Ujian

20,00 – 29,99

30,00 – 39,99

40,00 – 49,99

50,00 – 59,99

60,00 – 69,99

70,00 – 79,99

Jumlah

Frekuensi

4

9

25

40

28

5

111

Kelas Q₁ = kelas ke -3

1

=        +

4    − (∑     )_.= 39,995 + 27,75 − 13  . 10 = 45,895

25

Kelas Q₂ = kelas ke -4

1

=        +

2    − (∑     )_.= 49,995 + 55,5 − 38  . 10 = 54,37

40

Kelas Q3 = kelas ke -5

3

=        +

4    − (∑     )_.= 59,995 + 83,25 − 78  . 10 = 61,87

28

  =

− 2      +

−

=

61,87 − 2(54,37) + 45,895

61,87 − 45,895

= −0,06

Karena sk_B negatif (=−0,06) maka kurva menceng ke kiri dengan kemencengan

yang berarti.

3.    Koefisien Kemencengan Persentil

Koefisien Kemencengan Persentil didasarkan atas hubungan antar persentil (P₉₀,

P₅₀ dan P₁₀) dari sebuah distribusi. Koefisien Kemencengan Persentil dirumuskan :

(       −       ) − (        −       )

=

−

Keterangan :

sk_P = koefisien kemecengan persentil  , P = persentil

4.    Keofisien Kemencengan Momen

Koefisien  Kemencengan  Momen  didasarkan  pada  perbandingan momen  ke-3

dengan  pangkat  tiga  simpang baku.  Koefisien  menencengan  momen dilambangkan

dengan α3. Koefisien kemencengan momen disebut juga kemencengan relatif.

Apabila nilai α₃dihubungkan dengan keadaan kurva, didapatkan :

1) Untuk distribusi simetris (normal), nilai α₃= 0,

2) Untuk distribusi menceng ke kanan, nilai α3 = positif,

3) Untuk distribusi menceng ke kiri, nilai α3= negatif,

4)  Menurut  Karl  Pearson,  distribusi  yang memiliki  nilai  α3>  ±0,50 adalah  distribusi

yang sangat menceng

5)  Menurut  Kenney  dan  Keeping,  nilai  α₃  bervariasi  antara  ±  2 bagi  distribusi  yang

menceng.

Untuk mencari nilaiα3, dibedakan antara data tunggal dan data berkelompok.

a.  Untuk data tunggal

Koefisien Kemencengan Momen untuk data tunggal dirumuskan : 

1

α₃ = koefisien kemencengan momen

=        =

2 ∑(    −    )

b.  Untuk data berkelompok

Koefisien kemencengan momen untuk data berkelompok dirumuskan :

1

atau

=        =

2 ∑(    −    )

=       =

∑

− 3

∑

∑

+ 2

∑

dalam pemakaiannya, rumus kedua lebih praktis dan lebih mudah perhitungannya.

5.  KERUNCINGAN ATAU KURTOSIS

Keruncingan atau kurrtosis adalah tingkat kepuncakan dari sebuah distribusi yang

biasanya diambil secararelatif terhadap suatu distribusi normal.

Berdasarkan  keruncingannya,  kurva  distribusi  dapat  dibedakan  atas  tiga macam,

yaitu sebagai berikut :

1)    Leptokurtik

Merupakan distribusi yang memiliki puncak relatif tinggi.

2)    Platikurtik

Merupakan distribusi yang memiliki puncak hampir mendatar

3)    Mesokurtik

Merupakan distribusi yang memiliki puncak tidak tinggi dan tidak mendatar

Bila distribusi merupakan distribusi simetris maka distribusi mesokurtik dianggap

sebagai distribusi normal.

             leptokurtik

      mesokurtik

   platikurtik

Gambar 3. Keruncingan Kurva

Untuk mengetahui  keruncingan  suatu distribusi,  ukuran  yang sering digunakan

adalah koefisien kurtosis persentil.

1.    Koefisien keruncingan

Koefisien keruncingan atau koefisien kurtosis dilambangkan dengan₄(alpha 4).

Jika hasil perhitungan koefisien keruncingan diperoleh :

1) Nilai lebih kecil dari 3, maka distribusinya adalah distribusi pletikurtik

2) Nilai lebih besar dari 3, maka distibusinya adalah distribusi leptokurtik

3) Nilai yang sama dengan 3, maka distribusinya adalah distribusi mesokurtik

Untuk mencari  nilai  koefisien  keruncingan,  dibedakan antara  data tunggal  dan

data kelompok.

a.  Untuk data tunggal

1 ∑(    −    )

∝  =

Contoh soal:

Tentukan keruncingan kurva dari data 2, 3, 6, 8, 11 !

Penyelesaian : 

= 6;  s = 3,67

1 ∑(    −    )

2

3

6

8

11

Jumlah

1

5⁹⁷⁸

195,6

 -  

-4

-3

0

2

5

0

(   −   )

256

81

0

16

625

978

∝  =

                 = (3,67)⁼181,4 = 1,08

Karena nilainya 1,08 (lebih kecil dari 3) maka distribusinya adalah distribusi platikurtik.

b.  Untuk data kelompok

atau

∝  =

1 ∑(    −    )

∝ =

∑

− 4

∑

∑

+ 6

∑

∑

− 3

∑

2.    Koefisien Kurtosis Persentil

Koefisien  Kurtosis  Persentil  dilambangkan  dengan  K  (kappa). Untuk  distribusi

normal, nilai K = 0,263. Koefisien Kurtosis Persentil, dirumuskan :

1

Contoh soal :

=

2⁽−             )

−

Berikut  ini  disajikan  tabel  distribusi  frekuensi  dari  tinggi  100 mahasiswa

universitas XYZ.

a.  Tentukan koefisien kurtosis persentil (K) !

b.  Apakah distribusinya termasuk distribusi normal !

Tinggi Mahasiswa Universitas XYZ

Penyelesaian :

Tinggi (inci)

60 – 62

63 – 65

66 – 68

69 – 71

72 - 74

Jumlah

frekuensi (f)

5

18

42

27

8

100

  Kelas Q₁ = kelas ke-3

1.

1.100

=       +

4   − (∑     )_.= 65,5 +

4     − 23

42

. 3 = 65,64

  Kelas Q₃ = kelas ke-4

3.

3.100

=       +

4   − (∑     )_.= 68,5 +

4     − 65

27

. 3 = 69,61

  Kelas P₁₀ = kelas ke-2

10.

10.100

=         +

100 − (∑        )_.= 62,5 +

100    − 5

18

. 3 = 63,33

  Kelas P₉₀ = kelas ke-4

90.

90.100

=         +

100  − (∑       )_.= 68,5 +

100    − 65

27

. 3 = 71,28

1

Koefisien kurtosis persentil (K) adalah :

1

=

2⁽−             )

−

=

2 (69,61 − 65,64)

71,28 − 63,33      = 0,25

Karena nilai K = 0,25 (K<0,263) maka distribusinya bukan distribusi normal.